|
Den allmänna relativitetsteorins kärna består av Einsteins fältekvationer som i sin mest
kompakta form har utseendet
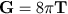 ,
eller med alla detaljer utskrivna ,
eller med alla detaljer utskrivna
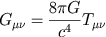 . Med hjälp av
denna till synes trivitala ekvation kan man få ut mer information än man troligen kan ur någon
annan känd ekvation. Högerledet består av, förutom konstanten 8 pi som är anpassad för att
approximativt stämma överens med övergången till Newtons mekanik, den s k stress-energi
tensorn . Med hjälp av
denna till synes trivitala ekvation kan man få ut mer information än man troligen kan ur någon
annan känd ekvation. Högerledet består av, förutom konstanten 8 pi som är anpassad för att
approximativt stämma överens med övergången till Newtons mekanik, den s k stress-energi
tensorn
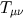 som
representerar hur materien i rumtiden beter sig. Vänsterledet representeras av
einsteintensorn som
representerar hur materien i rumtiden beter sig. Vänsterledet representeras av
einsteintensorn
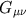 som kan sägas vara
ett genomsnitt av den allmännare riemanntensorn som kan sägas vara
ett genomsnitt av den allmännare riemanntensorn
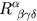 och representerar hur rumtiden beter sig rent geometriskt uttryckt med
differentialgeometri. Relationen lyder
och representerar hur rumtiden beter sig rent geometriskt uttryckt med
differentialgeometri. Relationen lyder
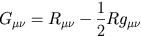 där R är riccitensorn, en sammandragning av riemanntensorn. Vi har här alltså en koppling åt
båda hållen mellan rummet och materien som befinner sig i det till skillnad från Newtons
klassiska mekanik som bara förklarar hur rummet påverkar materien.
där R är riccitensorn, en sammandragning av riemanntensorn. Vi har här alltså en koppling åt
båda hållen mellan rummet och materien som befinner sig i det till skillnad från Newtons
klassiska mekanik som bara förklarar hur rummet påverkar materien.
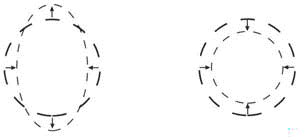
Riemanntensorn består av två komponenter; Weyltensorn som beskriver deformationen samt
Riccitensorn som beskriver storleksförändringen (Courtesy Penrose & Hawking).
|