


|
Det finns fyra huvudkategorier av matematiska lösningar till Einsteins fältekvationer som beskriver
svarta hål i naturen med olika stor grad av noggrannhet. Samtliga lösningar innehåller kombinationer
av de enda tre egenskaper som ett svart hål kan ha, nämligen massa, elektrisk laddning och
rotationsmoment. Rumtidens egenskaper omkring och inuti det svarta hålet beskrivs med
metriker som tar med fler eller färre av dessa tre egenskaper och
som väljas i olika koordinatsystem för att framhäva speciella egenskaper hos det svarta hålet. När
man avlägsnar sig från det svarta hålets omgivning så går alla metriker asymptotiskt över i
Minkowskis metrik som lyder
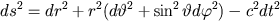 beskrivet
med sfäriska koordinater. Det är denna metrik som används inom den speciella relativitetsteorin,
d v s begränsningen av Einsteins allmänna relativitetsteori där rumtiden inte är krökt p g a materia
är närvarande i den. beskrivet
med sfäriska koordinater. Det är denna metrik som används inom den speciella relativitetsteorin,
d v s begränsningen av Einsteins allmänna relativitetsteori där rumtiden inte är krökt p g a materia
är närvarande i den.
-
Schwarzschild metriken: Denna lösning till Einsteins
fältekvationer är den matematiskt sett enklaste och mest idealiserade. Schwarzschildgeometrin
vid en symmetriskt distribuerad massa beskrivs av metriken
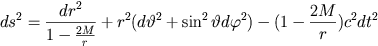 utanför Schwarzschildradien. Här finns två singulariteter, dels vid r=0 och r=2M. Singulariteten
vid r=2M är dock ingen egentlig singularitet utan bara radien där flykthastigheten överstiger
ljushastigheten; den apparenta singulariteten beror bara på ett dåligt valt koordinatsystem,
något som uppmärksammades först i och med användandet av Eddington-Finkelstein metriken på
1950-talet. Även innanför Schwarzschildradien existerar en explicit lösning vars metrik lyder
utanför Schwarzschildradien. Här finns två singulariteter, dels vid r=0 och r=2M. Singulariteten
vid r=2M är dock ingen egentlig singularitet utan bara radien där flykthastigheten överstiger
ljushastigheten; den apparenta singulariteten beror bara på ett dåligt valt koordinatsystem,
något som uppmärksammades först i och med användandet av Eddington-Finkelstein metriken på
1950-talet. Även innanför Schwarzschildradien existerar en explicit lösning vars metrik lyder
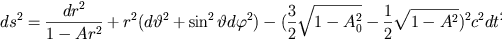 där där
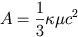 .
Här är kappa ytgravitationen och my något annat. Då man avlägsnar sig från Schwarzschildhålet,
eller massan M avtar till noll, så övergår metriken logiskt nog till Minkowskis eftersom
rumtidens krökning försvinner. Den så kraftfulla
Eddington-Finkelstein metriken har utseendet .
Här är kappa ytgravitationen och my något annat. Då man avlägsnar sig från Schwarzschildhålet,
eller massan M avtar till noll, så övergår metriken logiskt nog till Minkowskis eftersom
rumtidens krökning försvinner. Den så kraftfulla
Eddington-Finkelstein metriken har utseendet
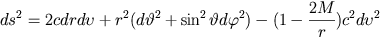 där där
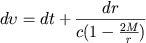 och
där fotoner som rör sig radiellt inåt beskrivs av dv=0. och
där fotoner som rör sig radiellt inåt beskrivs av dv=0.
-
Reissner-Nordström metriken: Hans Reissner samt Gunnar Nordström fann år 1916 respektive
år 1918 en lösning till Einsteins fältekvationer som de hoppades skulle ge en modell för
elektronen. Lösningen visade sig istället vara en generalisering av Schwarzschilds lösning som
beskriver ett svart hål som förutom massa dessutom har en elektrisk laddning Q (detta förstod
dock ingen förrän år 1960 då två av Wheelers studenter, John Graves och Dieter Brill, upptäckte
att den beskriver ett elektriskt laddat svart hål). Metriken lyder
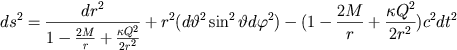 och när laddningen Q går mot noll så reduceras lösningen till Schwarzschilds. Denna lösning till
fältekvationerna är dock mest av matematiskt intresse eftersom de flesta makroskopiska objekt
saknar elektrisk laddning.
och när laddningen Q går mot noll så reduceras lösningen till Schwarzschilds. Denna lösning till
fältekvationerna är dock mest av matematiskt intresse eftersom de flesta makroskopiska objekt
saknar elektrisk laddning.
-
Kerr metriken: Denna lösning till Einsteins fältekvationer
beskriver ett svart hål med en massa M och ett rörelsemoment a. Metriken har utseendet
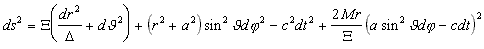 i
Boyer-Lindquist koordinater, där i
Boyer-Lindquist koordinater, där
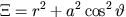 och och
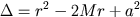 .
Denna lösning till fältekvationerna är den som är mest användbar vid praktiska
beräkningar på svarta hål eftersom dessa nästan alltid har ett stort rotationsmoment men inte
någon laddning. Singulariteten i ett roterande svart hål är inte formad som en punkt, vilket var
fallet för Schwarzschilds och Reissner samt Nordströms lösningar, utan som en ring. Mellan
horisonten och ergosfären (den statiska gränsen) befinner sig
ergoregionen (i figuren kallad för ergosfär). När
rörelsemomentet a går mot noll så övergår Kerrs lösning till Schwarzschilds. Detta innebär att
ergosfären och händelsehorisonten (yttre horisonten) sammanfaller samt att ergoregionen
försvinner. Det innebär även att ringsingulariteten övergår i en punktformad singularitet i r = 0. .
Denna lösning till fältekvationerna är den som är mest användbar vid praktiska
beräkningar på svarta hål eftersom dessa nästan alltid har ett stort rotationsmoment men inte
någon laddning. Singulariteten i ett roterande svart hål är inte formad som en punkt, vilket var
fallet för Schwarzschilds och Reissner samt Nordströms lösningar, utan som en ring. Mellan
horisonten och ergosfären (den statiska gränsen) befinner sig
ergoregionen (i figuren kallad för ergosfär). När
rörelsemomentet a går mot noll så övergår Kerrs lösning till Schwarzschilds. Detta innebär att
ergosfären och händelsehorisonten (yttre horisonten) sammanfaller samt att ergoregionen
försvinner. Det innebär även att ringsingulariteten övergår i en punktformad singularitet i r = 0.
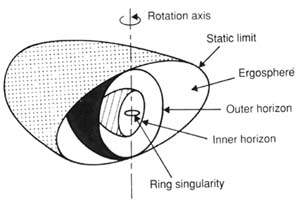
Beskrivning av ett roterande svart hål. Den yttre horisonten kallas även för händelsehorisont
och den inre horisonten för Cauchy-horisont (Courtesy Jean-Pierre Luminet).
-
Kerr-Newman hål: Kerr-Newman lösningen beskriver svarta
hål med massa M, rörelsemoment a och laddning Q. Denna lösning innefattar alla typer av svarta
hål men används inte eftersom makroskopiska objekt inte har någon laddning. Geometrin har nästan
samma utseende som i fallet för Kerrmetriken. Undantaget är att en term för laddningen adderas
till deltatermen som får utseendet
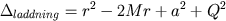 .
När laddningen Q går mot noll så övergår lösningen till Kerrs metrik och när rotationen
avstannar så övergår lösningen till Reissner-Nordströms. .
När laddningen Q går mot noll så övergår lösningen till Kerrs metrik och när rotationen
avstannar så övergår lösningen till Reissner-Nordströms.
Naken singularitet: Ett specialfall är om laddningen i ett Ressner-Nordström hål blir väldigt
stor så hamnar troligen händelsehorisonten innanför singulariteten som blottas. Det verkar dock
som om naturen hindrar nakna singulariteter från att existera, ett fenomen som brukar kallas för
kosmisk censur. Enligt de senaste
resultaten så är det teoretiskt möjligt för nakna singulariteter att bildas men lösningen är
instabil så den nakna singulariteten upphör genast att existera.
Lek med svarta håls egenskaper
Genom att variera det svarta hålets tre möjliga egenskaper kan man få en känsla för hur det
fungerar:
Ett svart hål har endast de tre egenskaperna massa, rotationsmoment samt laddning. Hos nästan
alla makroskopiska kroppar är dock den elektriska laddningen noll eftersom olikt laddade partiklar
drar till sig varandra.
|